2024年投資講座的資產配置秘密

 
作者：林彥安醫師

今年第二次的投資講座，我把焦點從指數化投資移往了資產配置的理念。畢竟指數化只是一個手段，最終能夠讓投資人運用的，還是要靠自己手上所擁有的配置組合。

指數化標的ETF

首先一開始先複習一下分散全球股市的構成方式，單一標的就是VT/FWRA(近年來成本比VWRA更低的選擇)。另外我所使用的是VTI+VXUS的組合，除了成本更低一些之外，這也是我在回測中發現到是可能比VT更優越的選擇。

要構成台灣股市的全市場組合一直都是一項挑戰，不只沒有單一全市場標的，用複數標的組合涵蓋的範圍也是有限的。台灣50=006208涵蓋60%大盤，中型100=0051涵蓋16%大盤，上櫃50=006201涵蓋4%大盤。全部買下來的話可以涵蓋80%的大盤，比例建議為20:5:1，只是006201佔比太小，省略不買也不會有什麼差別（而且Sharpe比0051差的多，不一定有利於資產配置）。

用正2涵蓋上市指數也是合理的選擇，不過不配息的正2是代表報酬指數而不是價格指數了。至於VXUS/VWO這些國際指數ETF，收錄的台灣股票範圍皆超過上述的股票型ETF，所以有這些國際ETF的人倒也沒有一定要加買，如果要持有台幣資產與迴避匯率風險的話則建議持有台股ETF。

美國公債ETF的選擇

自從升息以來，債券標的一直都是網路上展開爭論的焦點。我將常見的債券標的建議以上圖表示：

1. 全球總體債券：相信指數化概念也能用於投資債券全市場，那就會傾向買BNDW。
2. 中期美國公債：如果只相信債券的期限因子，不想承擔違約因子，那就會傾向買純美國公債。
3. 短期美國公債：以投資金律的建議為代表，為了迴避通膨對債券部位的長期傷害，只建議持有5年期以內的短債。至於現在短長天期殖利率倒掛，短債的報酬率反而比長債高，所以如果對債券沒有特別想法，我會推薦現階段配置短債也是等同送分題的選擇。
4. 長期美國公債：由於台灣的美國公債標的皆是長天期比較知名，然而持有長天期美國公債在近年遭到了部分的指數化投資KOL的攻擊。但我認為對長債的恐懼是一種迷思，因為20年公債就是一份期限因子，中期公債也至少是半份期限因子，如果長債不能拿，那中債也同樣不能拿。同樣性質的東西能拿半份為什麼不能拿一份？這在邏輯上是說不通的。而且上面說伯恩斯坦可是連中債都不推薦的。調查完早年大師的資產配置，短債＋長債可是熱門組合選項，這也代表若對於過長的到期日有恐懼，用其他短天期的標的縮短到期日即可平衡。

那麼股債的選項都清楚之後，下面就可以接續介紹各種資產配置範例。

永續投資組合

這是股債1:1的範例，很簡單的將四種資產平均四等份，但在後續的回測中擁有非常低的下跌幅度與標準差。

評論：加入與股債都低相關的黃金，抗跌性非常優良，但股票部位過低，會犧牲長期報酬的增長。

金蝴蝶

永續投資組合的小幅改良版，加入了小型價值股並五等分。除黃金之外的四等分，排列就像是蝴蝶的四個翅膀一樣。

評論：股債比來到6:4，預期報酬會比永續組合更好一些。

四季組合

這裡有很多網路文章都有誤解，以為這是所謂的全天候投資組合，其實四季組合只是全天候組合的前身而已。這是橋水基金創辦人瑞。達利歐隨口設計的比例，四季組合的意思是能夠對應所有經濟週期的狀況。債券的比重超過股票已頗有風險平價的樣子，另外也加入了等量的黃金與原物料。

評論：股票比例不足一半，長期報酬非常一般。

不過真正的全天候組合卻表現更差，也沒有完整標的可以複製，就不回測了。

巴菲特給一般人的建議

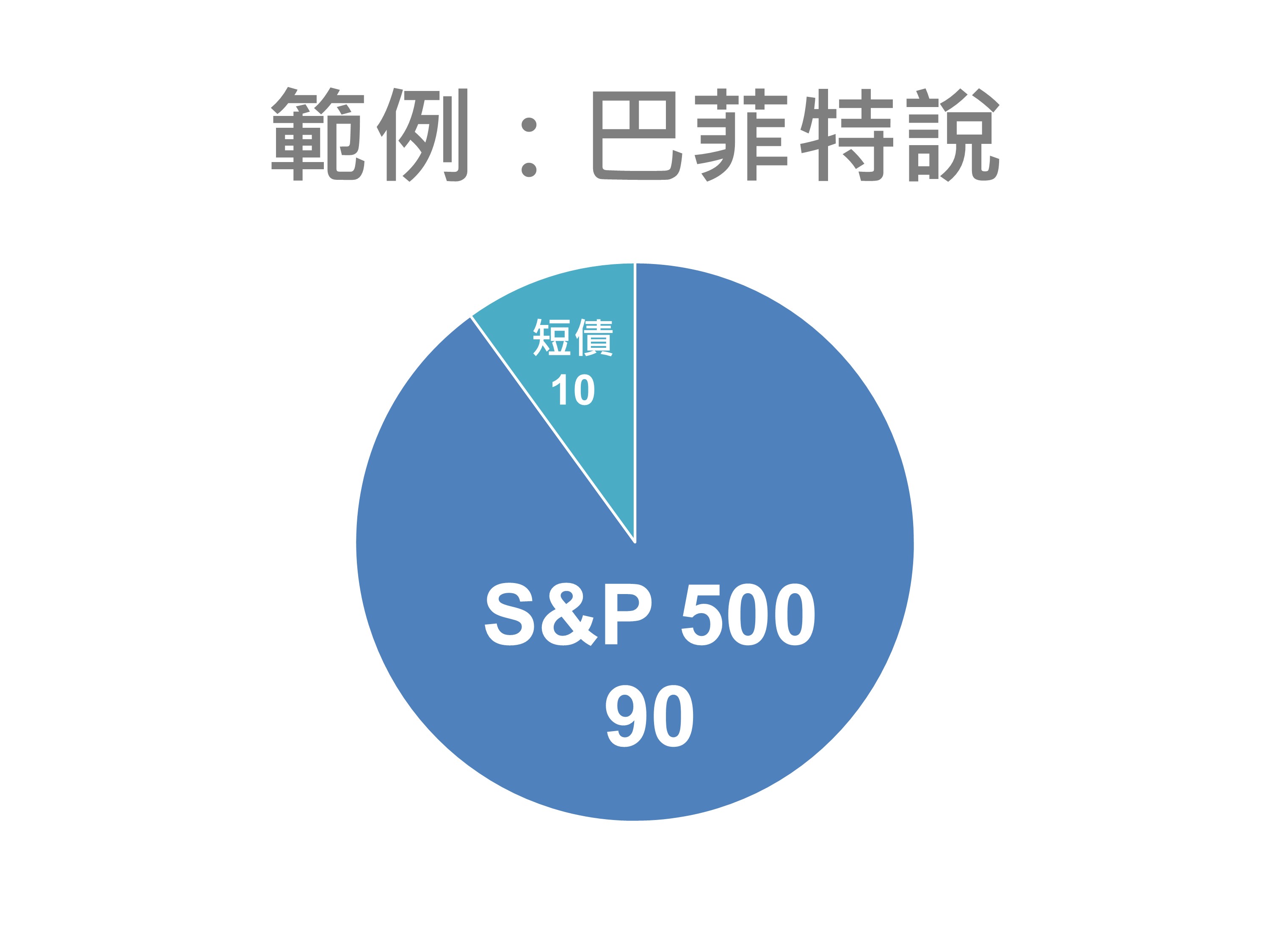
巴菲特曾多次向世人建議：一般人投資S&P 500指數就好了，並囑咐家人把剩下10%的資產投資在短債，形成這個股債9:1的建議。

評論：重壓九成的美股真的很奸詐，這樣誰贏的了。

柏格頭三基金

堂堂柏格頭論壇所推崇（不是柏格本人的意思），看似平凡無奇的美股＋國際＋美債三項組合，然而回測的表現卻遠超我的預期，年化報酬竟然可以長期在7~8%以上....。

評論：證明資產配置大道至簡的最佳代表，我的終身之敵。

漫步華爾街的中年範例

這是50年經典著作漫步華爾街在書中所列舉的資產配置之一，目標對象設定為30~50歲之間的中年人。由於在資產累積期，給予了75%的高比例股票，美國與國際比例對分，並加上10% REITs，並包含5%的現金。

評論：看到後面就知道了.......。

投資金律二版

在台灣的投資金律二版之中，作者給了兩種資產配置建議：穩健的股債64和積極的股債82範例，這裡舉的是8:2的範例。喜歡複雜配置的伯恩斯坦又給予了高預期報酬的小型價值股，以及能應對高通膨時期的貴金屬與能源股票。

評論：嗯......複雜真的沒有比較好。

殘酷回測大評比

回測17年的資產配置大評比，以美國的股債64為主要標竿。除了股債91的巴菲特組合績效最好，可以發現績效並沒有和股債比成正比。Sharpe ratio最高的組合出現在股債64左右，發現柏格頭三基金的表現其實相當不錯，名列前茅。

但＜漫步華爾街＞精心推薦的配置方法，無論是績效或是Sharpe ratio都吊車尾，連全球股債64都輸。我相信作者肯定沒有做回測.....看來大師學問再厲害，實作起來也未必較強。

看來股債比似乎是一種迷思，影響報酬效率的主要因素並不在於股債比。兩種配置大量黃金的金蝴蝶和永續投資組合，擁有非常小的跌幅與標準差，Sharpe ratio也是位於最高等級。

排除加入原物料指數的組合，最多可以回測到30年之久，這下應該可以排除大部分的干擾因素了。結果前三名完全不變，柏格頭三基金第二名，股債64第三名，雖然柏格頭三基金是近年才有的概念，但完全經得起時代的考驗。

以高防禦力著稱的永續投資依舊拿下最小下跌與標準差，分散均衡的金蝴蝶則是全體最佳Sharpe。總之，這些經典配置方式在過去歷史的回測中都證明了自己的價值。

相比之下就算不談＜漫步華爾街＞，＜投資金律＞真的有點像小丑，Sharpe 也不好，以穩健著稱的股債64版本也沒有在Sharpe勝過股債82版本（增加債的結果只是白白損失效率），或是沒有勝過任何一版的股債64配置。也就是說＜投資金律＞和＜漫步華爾街＞這兩本書給出的建議，反而讓效率更低，他們肯定沒做回測。

（我可以斷言，在歷史的長河中Sharpe沒有到達0.4的配置，根本就不用看。）

（對了我的同期夏普可是有0.42，而且這是在沒有動能標的的不完全模擬之下）

三種很難贏的組合

所以現在即使不看巴菲特的建議，有三種放到現在都很難贏，顛樸不破的組合：

1. VT: 也就是美國國際6:4
2. 美國股債6:4
3. 柏格頭三基金: 美國60%+國際20%+美債20%

他們在歷史回測中跑出的線圖是三條幾乎重合的線(上圖)

這怎麼可能？它們股債比本身就不一樣啊？VT是100%股，64是60%股，柏格頭是80%股。不是說90%的報酬差異來自於資產配置嗎？不同股債比跑出的結果一樣到底是？

我認為報酬差異來自於資產配置還是對的，只是其中的關鍵不是股債比，而是－－美股的比例。我大膽推論，就長久的歷史回測來看，報酬差異主要會來自於美股比例的差異。所以就理論上而言，要贏過VT其實很簡單，用VTI+VXUS，然後把美股的比例設高於VT就好了（我還沒算進成本差距）。

從發現這件事的那一天起，我就不再提股債比了。

那其他的分散用資產又是如何呢？國際股市vs總體美債vs長期美債

可以看到長債(綠)長期而言還是不錯的，報酬率和Sharpe ratio都高於國際股市(橘)，只要不遇到通膨什麼都好。美國整體債券(藍)與國際股市雖然波動性有差別，但報酬率差不多。

也就是說美國股市無論是搭配國際股市或債券，並不會影響太多報酬。這樣話說回來，VT也並非是最好的設計，因為那40%的國際股市並沒有提升效率，把一半拿去換債券都還能降低波動。

最佳台股比例如何設定？

假設我們上面的發現是對的－－美股比例最為重要，那要如何根據美股的比例，來設定自己要加入多少台股呢？我想引用兩大理論來解決這個問題：效率前緣和風險平價。

效率前緣的意思就是最佳Sharpe ratio（風險報酬效率），風險平價就是把各部位的風險均等化（只求風險相等）。立論在於：效率前緣求最佳比例，風險平價求上限比例。回測條件：美股使用VTI，台股使用近年表現較佳的FLTW。不過換成EWT求最大回測年限，結果也差不多。

根據效率前緣計算機，最佳的美台比例為77:23（最低風險取得最高報酬）；根據風險平價計算機，美台風險均等為54:46（美股和台股風險相等的比例）。也就是說，相對於美股，台股整體比例可以介於23%~46%之間。

23%是效率前緣，如不是23%代表報酬效率較低；46%是風險平價，如高於46%代表單一風險過高。23~46%之間代表台股比例過高讓效率下降，但並不會讓台股的風險超過美股，風險仍在可以接受的範圍。

不過要注意的是，這裡拿來衡量的台股風險，是指系統性風險。台灣在政治地緣方面的非系統性風險，我認為至今無法以量化方式衡量。

至於如何根據VT的美股比例，來把台股加入VT？我都幫大家算好了，15.2%是效率前緣，33.8%是風險平價，台股可以介於15.2%~33.8%之間。相信這條發現的含金量應該有超過一百萬了。

結論：資產配置回測的重要發現

1. 永續投資組合和金蝴蝶的抗跌能力與風險效率有通過長期歷史考驗。
2. 柏格頭三基金能夠輕鬆勝出各種複雜的配置組合，推薦給新手。
3. 美股的比例可能決定了大部分的報酬率與風險效率。
4. 台股的最佳比例可以考慮以效率前緣和風險平價來計算。

衍伸文章

2024年投資講座的六大心法